Table of Contents
- Statement of Hooke’s Law
- Experimental Verification of Hooke’s Law:
- Important Point Regarding Hooke’s Law
From experimental investigations, Robert Hooke, an English physicist (1635-1703 A.D.), formulated in 1679 a law known after him as Hooke’s law which states that the extension produced in a wire is directly proportional to the load applied.
In 1807, Thomos Young pointed out that the strain is proportional to the extension of the wire and the stress is proportional to the load applied. He, therefore, modified Hooke’s law to the more general form as follows:
Statement of Hooke’s Law
Within the elastic limit, the stress is directly proportional to strain. Thus, within the elastic limit,
Stress ∝ Strain
or Stress = Constant × Strain
The constant of proportionality is called modulus of elasticity or coefficient of elasticity of the material. Its value depends on the nature of the material of the body and the manner in which it is deformed.
Experimental Verification of Hooke’s Law:
As shown in Figure, suspend a metallic spring from a rigid support and attach to its lower end a pan and a pointer.
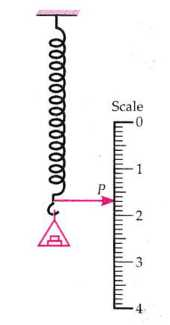
Arrange a scale in the vertical position so that a pointer is able to move along it.
Read the position of the pointer on the scale when the pan is empty.
Place a weight of 50 gram in the pan.
Note the position of the pointer on the scale.
The difference between the two readings gives the extension produced in the spring by the weight added in the pan.
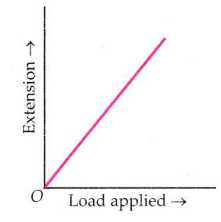
| Increase the weight in the pan in steps of 50 gram and note the corresponding extensions. Plot a graph between the extension of spring and the total load producing it. The graph is a straight line, as shown in above figure. This indicates that extension ∝ load applied. This verifies Hooke’s law. |
Important Point Regarding Hooke’s Law
Like Boyle’s law, Hooke’s law is one of the earliest quantitative relationships in science.
Hooke’s law is valid only in the linear position of the stress-strain curve. The law is not valid for large values of strains.
Stress is not a vector quantity since, unlike a force, the stress cannot be assigned a specific direction.
When a wire, suspended from a ceiling, is stretched by a weight (F) suspended from its lower end, the ceiling exerts a force on the wire equal and opposite to the weight F. But the tension at any cross-section A of the wire is just F and not 2F. Hence the tensile stress which is equal to the tension per unit area is equal to F / A.
