Table of Contents
Streamline flow
When a liquid flow such that each particle of the liquid passing a given point moves along the same path and has the same velocity as its predecessor, the flow is called streamline flow or steady flow.
Consider the flow of the liquid along the path ABC; where A, B and C are the points inside the liquid. If every successive particle passes through point A with constant velocity vA directed along tangent at A, then through point B with constant velocity vB directed along tangent at B and then through C with constant velocity vC, the flow is said to be steady, orderly or streamlined. The path ABC along which the particles move one after another is called a streamline. The particle velocity at a particular point remains constant with time but velocities at different points may or may not be the same. Streamline flow is possible only if the liquid velocity does not exceed a limiting value, called critical velocity. The fixed path followed by an orderly procession of particles in the steady flow is called a streamline. In Fig., the curve ABC represents a streamline. A streamline may be defined as the path, the tangent to which at any point gives the direction of the flow of liquid at that point.
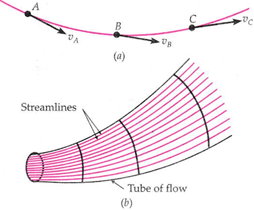
Tube of flow
A bundle of streamlines forming a tubular region is called a tube of flow. The boundary of such a tube is always parallel to the velocity of fluid particles. No fluid can cross the boundaries of a tube of flow, and the flow tube behaves somewhat like a tube. In a steady flow, the shape of the flow tube does not change with time.
Turbulent flow
When the liquid velocity exceeds a certain limiting value, called critical velocity, the liquid flow becomes zig-zag. Tire path and the velocity of a liquid particle changes continuously, haphazardly.
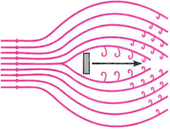
This flow is called turbulent flow. It is accompanied by random, irregular, local circular currents called vortices. As shown in Fig., a jet of air striking a flat plate placed perpendicular to it causes a turbulent flow.
Properties of streamlines
(i) In a steady flow, no two streamlines can cross each other. If they do so, the fluid particle at the point of intersection will have two different directions of flow. This will destroy the steady nature of the fluid flow.
(ii) The tangent at any point on tire streamline gives the direction of velocity of fluid particle at that point.
(iii) Greater the number of streamlines passing normally through a section of the fluid, larger is the fluid velocity at that section.
(iv) Fluid velocity remains constant at any point of a streamline, but it may be different at different points of the same streamline.
